About Domain Specifications in HL7

Gunther Schadow

The Regenstrief Institute

October 2, 1998

See also: Revision of the Domain Specification Information Model.

Preface

I originally wanted to be silent on the domain specification issue, but the attention that it has received lately and its growing impact on the HL7 specification forces me to speak out now.

While (because) I acknowledge the importance of domain specifications, I have several concerns here. The whole discussion and the proposal is a bit too detailed, prematurely detailed. This may be due to the nature of ASN.1, that does not know about abstraction. I guess I want to dwell a little bit more on the semantic level before we go ahead defining abstract (let even concrete) syntaxes.

Particularly I do not like to see concrete HL7 data types being used here.

Background: In Dan Diego, CQ has formed a task force group to revise HL7 data types for version 3. We are going to have phone conferences on that and we will present a complete draft specification in January. This task force group includes Stan Huff, Mark Shafarman, Mark Tucker, myself and others. I also would like to have at least one MNM leader and Wes Rishel to observe this process and provide their valuable perspective.

I want to avoid tightening the use of v2 data types in any v3 specification we are going to build. It is true, the data type revision comes pretty late, but it does come, and it is much easier if we do not create premature "backwards compatibility" issues by using v2 data types.

The problem with v2 data types is that we know a lot about their structure, but pretty little is known about their semantics. This is v2 legacy that I do not want to blame here. I just want to ask you to give us 16 weeks (until Orlando) to step back and rethink the data type issues. A particularly touchy area is CE, ID etc. That discussion smokes since end of last year now, and was always delayed but never settled. I am glad about the opportunity we have now to finally settle the issue within a tight time frame.

I do not want to totally break out the domain specification proposal, only the overly concrete results that are being presented and discussed at the moment. I think that the domain specification stuff is indeed very important - so important that it does not deserve any confusion. Some heavily discussed topics are im my oppinion so simple that they do not deserve this much attention, while others are quite difficult that we should talk more about those.

This posting is accompanied by a ZIP file containing a UML model as a Rose mdl file, a PostScript file, a PDF file and a GIF, so that you can pick what you can best digest. You can fetch all those files from http://aurora.rg.iupui.edu/~schadow/domsp

The Easy Things

A domain (code system, terminology, vocabulary) is a set of symbols. When we specify domains, enumerate, include and exclude, we essentially deal with set algebra. This is pretty general and is well understood. We do not have to reinvent the wheel here, and we should not do so.

Essential set operations for our purpose are the union operator (I use the symbol `+' here, the conventional symbol is the U upside-down) and the difference operator (I use `-', the conventional symbol is the reverse solidus `\').

Although I use the operator symbols `+' and `-', set algebra is different from numeric algebra. The reason is that elements in sets do not repeat.

Just as the addition of integer numbers, the union operator + is:

• associative: ( A + B ) + C = A + ( B + C )
• commutative: A + B = B + A
• there is also a neutral element {}, i.e. the empty set.
• but there is no general inversion of the union operation, i.e., let C = A + B, then A = C - B does not follow in general.

Example:

{ a, b, c } = { a, b } + { b, c }

{ a, b, c } - { b, c } = { a }

A + A - A = {}

Aside from this caveat, there are still similarities with integer algebra:

A - B - C = A - ( B + C )

A + B - C = A + ( B - C )

{ a, b } + { b, c } - { b }   =   { a, c }

{ a, b } + ( { b, c } - { b } ) = { a, b } + { c }   =   { a, b, c }.

There are other set operations, which I will not go into here, because union and difference are enough for what we need: inclusions and exclusions.

Summary of The Easy Things

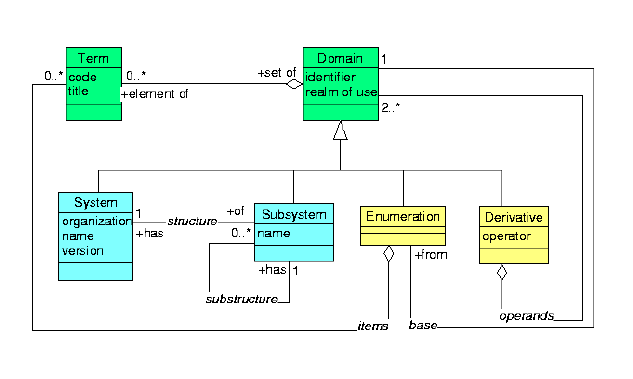
1. A code system, classification, vocabulary, terminology, or domain, all have a common generalization: to be a set of terms. Thus, in a meta model, we should show those two essential concepts: a domain as a set of terms.

2. Inclusion and exclusion of terms are defined by the general rules of set algebra, with its caveats as explained above.

Constructing a Model

Now, I construct a model that reflects these high-level semantic properties of our problem: the essential classes of the model are TERM and DOMAIN, because this is what domain specifications is all about, to specify the domains such that I can say which term belongs to a given domain.

Note that the class TERM is not necessarily instantiated in a data base sense. So, please don't criticise this model by saying "you don't want to store millions of terms in your specification" - in fact we are not even allowed to do so or we risk to be sued for copyright infringement. But the model does talk about terms (and so does Stan's and Woody's models) so we have to make them explicit. This also saves us from using the "CE" data type in the model.

In fact, the element-set aggregation is a "virtual" relationship. It is not actually instantiated and you can not follow this link it in a database sense. There are code systems in which you can not enumerate all terms - infinite sets. The element-set aggregation between TERM and DOMAIN is thus not technically "useful," although it is quite important in order to nail down the semantics. A domain need not be a finitely enumerable set; because of this I defined the Enumeration as a subclass of Domain. But see below.

We all know that there might be different specializations of domains, e.g., Stan's proposal and Woody's meta model together talk about CompleteDomain, JurisDomain, ValueSet, Class, Item and Scheme. These are all sets, and should thus appear in a meta model as connected to a generalization. This allows us to generally deal with the set operations (i.e., inclusion, exclusion).

How many different special domains do we have to consider?

I find the following four important differences to make:

1. SYSTEM

An externally defined coding system (appears as "scheme" in Stan's proposal). Examples are: SNOMED, READ, ICD, ICPM, ICPC, CPT4, LOINC, ISO 639-1, IUPAC enzyme codes, .... The general idea is that these are coding systems published by an organization that provides meaning to the codes, maintains the system, etc. The essential attributes of the class System are:

organization

e.g., ACP, WHO, ISO, Regenstrief, etc.

name

e.g., SNOMED, ICD, 639-1, LOINC, etc.

version

e.g., ICD-9 vs. ICD-10

I call this "code system," because it implies that these sets are not just sets of symbols, but only here symbols are given meaning. Without those systems, nothing else makes sense in domain specifications, that's why I gran't those the right of their own meta-model class (Stan's scheme was just an attribute), and that's why I selected a name that suggests whole-ness, organized-ness, and importance: "system."

2. SUBSYSTEM

Most code systems have an inner structure. Structure can generally be expressed in set algebra using the subset relation. A subsystem is such a subset in the overall system that is defined by the organization that published the system. For example: SNOMED axes are subsystems, ICD, ICPC and ICPM chapters and sections are subsystems. Although LOINC does not have chapters, it has many subsystems given by the logic of LOINC. I.e. LOINC allows to define the class of all tests on specimen BLDV (venous blood).

The "class" concept that Stan uses (without really defining it) is possible only through the structure of the underlying coding system. This is a very tricky part. Remember, without further knowledge, the elements in a set are not ordered. Therefore, there is no semantics of a range such as "everything from cough to pneumonia." Some systems are kind of ordered, i.e. ICD, but others like LOINC are not. There is no useful meaning to all LOINC codes from 3456 to 6758. Only the unique structure of the code system allows us to conceive "classes" and express them in ways that are unique to the coding system.

3. DERIVATIVE

A derived domain is usually a subset of another Set. Defining derivatives is all that the inclusion and exclusion business is about. Derivatives can exist on different levels: e.g., in the realm of an institution (hospital department), a country (USA), a treaty (EU), and so on. Thus, each derivative can be defined on another derivative in a larger realm (e.g., a german hospital narrows the domain defined by the EU that in turn may be a subset of a WHO code).

While System and Subsystem are defined externally, domains must be explicitely defined. This is what domain specifications are all about. Thus, the inclusion, and exclusion applies only to Derivatives:

This means, we define a derivative as a domain that comes about by applying an operator to two (or more) other domains (operands). The operators defined right now are union (+) and difference (-) as explained above, but this construct provides the flexibility to do more things. For instance, we could use it to specify a domain as the common subset of two derivatives defined based on a common system (intersection).

Note that in a complex set algebra expression, such as

A + ( B - C ) + { a, b },

A + B + C + D + ( E - F - G - H )

1. (+ A B C D)
2. (- E F G H)
3. the union of both.

Some people have argued for doing all exclusions after all inclusions, in fact, this seems to have reached a state of agreement. If you want to adhere to this order, you require that all set expressions conform to this pattern:

( I1 + I2 + ... + In ) - ( E1 + E2 + ... + En )

4. ENUMERATION

While large code systems are impractical to enumerate, and while some are unenumerable at all, enumeration is useful for small domains. E.g., if all we want is just the phenotypical gender based on SNOMED, all we need to do is to enumerate those codes from SNOMED: male, female, etc. Notably my above examples using curly braces such as { a, b, c } specified sets by enumeration. Special case are the empty set {} and the set with just one element { a }.

The one element set is what Stan called "Item." Note that in order to deal with a single element in a set algebra, we first have to "upgrade" the element a into the trivial set { a }, then we can build unions and differences as defined.

The Difficult Things

Can you mix two code systems?

My model does not allow you to mix different sets in an enumeration, but it does in principle allow to build the union of SNOMED and ICD-10. In selected cases, mixing two code Systems may make some specific sense, that's why we do not have to make the model more complex just to forbid this.

How do we specify a Subset (Stan's "classes") in some uniform way?

The proposed solution

is certainly not the last word. Here is the entrance point of non-interoperability, and this is one reason why I don't like the ASN.1 way of life. When we are about to define a semantic world of concepts and relationships, VisibleString is of little help.

Remember, some codes have axes (SNOMED), some have a hierarchy of chapters and sections (ICD, ICPM), while some have none of this (LOINC). On the other hand, LOINC is a database of rich knowledge, which allows us to build equivalence classes on the fly. If you want you can think of those equivalence classes as relations returned by SELECT statements in SQL:

The WHERE-clause is where the shugar is!

Notably, ranges of codes are not meaningful in many code systems. These things are so tricky that it is almost impossible to deal with them in a uniform computer processable way. But my model-class "Subsystem" contains this problem somehow. Every code System comes with a predefined set of Subsystems (e.g., SNOMED comes with axes). We may also want to say that a given domain may be "ordered."

But what does "ordered" mean after all? It means that the lexical structure of the code symbols somehow relates to the conceptual structure of the code system. But remember that this is highly dependent on special cases. I.e., while some sections on SNOMED axes might be ordered sensibly, a range that spans over two classes might not make sense. It does not make sense to say "use SNOMED axes D thru M." This is why I think that "Class ::= VisibleString" is in fact harmful to finding a good solution.

Are you allowed to produce all kinds of derivative sets and be sure that they still make sense?

Call for Use Cases

Concepts

(e.g., diseases, genders, organisms, message types, order control codes)

Instances

(e.g., people, locations, e-mail addresses)

Instances are type V according to Stan's classification of codes. He rightfully is not concerned with those.

On the level of concepts we have to distinguish between:

Real World Concepts (RWC):

(e.g., diseases, genders, organisms) difficult to define, semantics to discuss about, several views on the world bring about several coding systems, comparability and translation is generally problematic but possible to some extent. "Synonyms"

Technical Concepts (TC):

(e.g., message types, order control codes) easy to define, definition is found in a model, no discussion about the "meaning" of technical terms, rather there is no "meaning" at all but only function (i.e., pragmatics) in the model. E.g. to define an order control code, we have to show our state transition model of an order and be done with it. No discussion, about "meaning," just function. Translation is impossible in principle, no synonyms. However, sometimes we can define a common model and build a machinery that "translates" between two "code systems" based on that common model. But this translation is purely functional.

Although I think that RWCs and TC have very little in common, they both deal with domains as sets of symbols where each symbol refers to some "meaning" defined somewhere outside. Because this is so, these things come together in the domain specification business, to which I hope to have made a useful contribution.