October 7, 1998
After having sowed the seeds of arguments through my initial comment on domain specifications, I feel obliged to follow on with further concrete and constructive contributions.
Also I am not "chairing" the domain specification group, I suggest that we follow up on and conclude the discussion on the domain specification information model. As of now, we have two competing models out there and we would need to merge them back into one we all agree on.
We can use the fundamental idea behind the whole MDF approach to derive everything else from that model: domain specifications are instance graphs of the domain specification model. Any domain specification syntax will be a "wire form" of a domain specification instance graph. I guess that our domain spec. syntax will look different from any of our HL7 message syntaxes. It would look more like a programming language, especially it would include expressions to do all this set arithmetic. However, I still think that a sound information model is the starting point and any discussion about syntax is premature. So, here goes
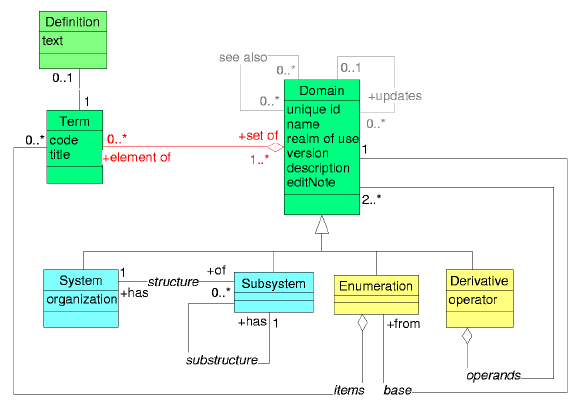
In order to foster an agreement, I have reworked my simplistic model so as to include the details used by Stan and shown in Woody's model. I used Stan's proposed ASN.1 and Woody's reversely engineered model as input and mapped every data element to my model. It turned out that my model wasn't so simplistic after all, as you can easily find out by looking at my original model.

| Figure 1: The information model for domain specification that supports Stan's ASN.1 and Woody's UML model. |
|---|
| The Rose model can be found here. |
The following table shows a complete data element mapping between Stan's ASN.1, Woody's UML and my UML:
| STAN | WOODY | GUNTHER |
|---|---|---|
| CompleteDomain | CompleteDomain | Domain |
| c.D.Name | name | name |
| c.D.Id | id | unique id |
| c.D.Version | version | version |
| c.D.Descript | description | comments |
| editNote | editNote | editNotes |
| domains (SET OF) | has_domain (1..*) | |
| CountryDomainSpec. | JurisDomainSpec. | (is a Domain) |
| country | juris | realm of use |
| cn.D.Name | name | (inherited) |
| cn.D.Id | id | (inherited) |
| cn.D.Version | version | (inherited) |
| cn.D.Descript | description | (inherited) |
| editNote | editNote | (inherited) |
| valueSets (SET OF) | has_valueSets (1..*) | |
| ValueSet | ValueSet | (is a Domain) |
| scheme | schemeID | System.unique id) |
| schemeVersion | schemeVersion | System.version) |
| v.S.Name | name | (inherited) |
| v.S.Id | id | (inherited) |
| v.S.Version | version | (inherited) |
| v.S.Descript | description | (inherited) |
| editNote | editNote | (inherited) |
| content | includes | |
| excludes | ||
| Content | Derivative | |
| includeItem | Inclusion | operator |
| includeClass | type | union |
| excludeItem | value | difference |
| excludeClass | ||
| Exclusion | ||
| Item | type | Enumeration |
| visibleString | value | items-Term |
| Class | ||
| visibleString | type: {item, class} | Subsystem |
| value: String | name | |
| (IncludeAll) |
While Stan's abstract syntax and Woody's model are structurally equivalent (except at the bottom) my model is structurally quite different. Through inheritance I need to specify much less attributes. So I have more spare-complexity to spend on enhancements. My enhancements are:
Domain is clearly the subject class of our problem space. A domain is a set of terms. Domain specifications are about, specifying the domains such that we can tell whether a given term belongs to a given domain.
Note that the class term is not necessarily instantiated in a data base sense. Of course we do not want to store millions of terms in our domain specification database - in fact we are not even allowed to do so or we risk to be sued for copyright infringement. But the problem space does include terms so we have to make them explicit in our model.
In fact, the element-set aggregation is a virtual relationship. It is not actually instantiated and you can not follow this link it in a database sense. However, you can prove whether or not a given term belongs to a given domain, i.e. whether such a virtual association exists between those two given instances. The element-set aggregation between term and domain is thus not technically "useful," although it is quite important in order to nail down the semantics. There are code systems in which you can not enumerate all terms - infinite sets (i.e., the code for units of meauses is such an infinite set). A domain need not be a finitely enumerable set; because of this the enumeration is defined as a subclass of domain. But see below.
There are different specializations of domains, e.g., Stan's proposal and Woody's meta model together talk about CompleteDomain, Country- or Juris-Domain, ValueSet, Class, Item and Scheme. These are all sets, and thus appear in this model of figure 1 as connected to a common generalization, the domain. This allows us to generally deal with the set operations (e.g., inclusion, exclusion).
An externally defined coding system (appears as "scheme" in Stan's proposal). Examples are: SNOMED, READ, ICD, ICPM, ICPC, CPT4, LOINC, ISO 639-1, IUPAC enzyme codes, .... The general idea is that these are coding systems published by an organization that provides meaning to the codes, maintains the system, etc. The essential attributes of the class System are:
I call this "code system," because it implies that these sets are not just sets of symbols, but only through those code systems symbols are given meaning. Without those systems, nothing else makes sense in domain specifications.
Most code systems have an inner structure. Structure can generally be expressed in set algebra using the subset relation. A subsystem is such a subset in the overall system and defined by the organization that published the system. For example: SNOMED axes are subsystems, ICD, ICPC and ICPM chapters and sections are subsystems. Although LOINC does not have chapters, it has many subsystems given by the logic of LOINC. I.e. LOINC allows to define the class of all tests on specimen BLDV (venous blood).
The Stan's "class" concept is possible only through the structure of the underlying coding system. This is a very tricky part. Remember, without further knowledge, the elements in a set are not ordered. Therefore, there is no semantics of a range such as "everything from cough to pneumonia." Some systems are kind of ordered, i.e., ICD, but others, such as LOINC, are not ordered. There is no useful meaning to "the set of all LOINC codes from 3456 to 6758." Only the unique structure of the code system allows us to conceive "classes" and express them in ways that are unique to the coding system.
A derived domain is usually a subset of another set. Defining derivatives is all that the inclusion and exclusion business is about. derivatives can exist on different levels: e.g., in the realm of an institution (hospital department), a country (USA), a treaty (EU), and so on. Thus, each derivative can be defined on another derivative in a larger realm (e.g., a german hospital narrows the domain defined by the EU that in turn may be a subset of a WHO code).
While system and subsystem are defined externally, derivatives must be explicitely defined. This is what domain specifications are all about. Thus, the inclusion, and exclusion applies only to derivatives.
+--------+ 2 ..--<>| DOMAIN |------------+ +--------+ | A | | | ...-----+--... | | | +------------+ | | DERIVATIVE |<>------+ +------------+operands | operator | +------------+
This means, we define a derivative as a domain that
comes about by applying an operator to two (or more) other
domains as the operands of the operation. The
operators defined right now are union (+)
and difference (-) as explained here. But this construct provides the
flexibility to do more things. For instance, we could use it to
specify a domain as the common subset of two derivatives defined based
on a common system (intersection).
Note that in a complex set algebra expression, such as
Some people have argued for doing all exclusions after all inclusions, in fact, this seems to have reached a state of agreement. If you want to adhere to this order, you require that all set expressions conform to this pattern:
While large code systems are impractical to enumerate, and while some are unenumerable at all, enumeration is useful for small domains. E.g., if all we want is just the phenotypical gender based on SNOMED, all we need to do is to enumerate those codes from SNOMED: male, female, etc. Notably my above examples using curly braces such as { a, b, c } specified sets by enumeration. Special case are the empty set {} and the set with just one element { a }.
The one element set is what Stan called "Item." Note that in order to deal with a single element in a set algebra, we first have to "upgrade" the element a into the trivial set { a }, then we can build unions and differences as defined. However, items are also the terms that constituate the enumeration.
To be continued...