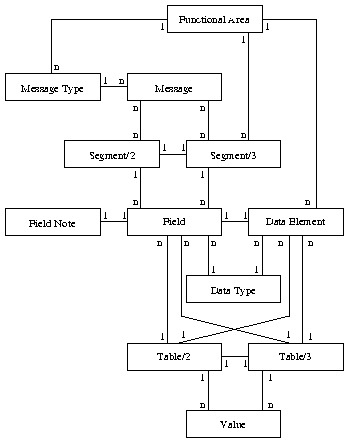
Figure 2: Model of the HL7 data base before optimization
In the following table, we give a synopsis of all relations, that we have got so far. We tried to somehow compress the names of the items here, to be specific and descriptive as well as short, in order to not loose oversight. Primary keys to the relations are are marked by preceding asterisks (`*'), while other candidate keys are marked with a plus (`+'). If a primary key is made up of more than one attributes, they are set in parentheses with one preceding asterisk. The name of the relation is followed by an `[A]' which means, we have drawn this relation from appendix A or a `[C]' telling that it was drawn from the chapters (including appendix C(3)).
The rows of the above table are sorted to ease orientation of the reader. Therefore, one thing becomes immediately obvious: There are sometimes more than one relation with the same name. Even though, they both are titled `Segment', they are not the same relation because they don't have the same cardinality.(5) This notwithstanding, it is still obvious that these relations have some domains in common. We can simplify our set of relations by rewriting it such, that any two relations which correspond this way are replaced by a third one which is defined over any domain, which is part of either the first or the second relation.
However, different names of two tables do not guarantee that they do not correspond the same way, as was just said. Consider `Data Element' and `Field'. Both are defined over the same domains by different order, except from `FunArId' (i.e. the column titled `owner' in appendix A, and lists the functional area, to where it belongs) and `FldNum'. The question is now, if tuples of both relations can be mapped one to one. We will see below (see section Consistency check), that they can.
The name `Field' was given in `exseg.awk', since the word `field' is used throughout the HL7 specification to designate the parts of which the segments are built (more than 500 occurences). However `data element' is used sometimes (42 occurences) as well. Why are there two names for the same thing? One answer might be, that `data element' is used where we refer to an atom of data regardless of the context in which it occurs, while `field' is used, for such an atom in the context at a certain place of a certain segment. Thus a data element is the contents of a field. In deed, the relation `Data Element' doesn't have a domain, which could designate a certain place in a segment.
However, why is there an attribute for repeatability and optionality then? We wouldn't expect an object to be optional per se, whereas a certain field in a segment may well be empty sometimes. Also repeatability is no property of a data element from this point of view, even though it depends on how we think of an repetition: Does the field repeat or does it's contents repeat in the field? If the first was true, then a segment would not necessaryly be of a fixed number of fields,(6) if the second is true, then there must be something in between a field and an atom of data, we could say, that an `occurence' is not identical to a data element. This resembles LISP's point of view: LISP would regard a field of a segment like one half of a pair, which can be a list (i.e. another pair), or an atomic data item. If we have a look at the encoding rules,(7) we notice, that repetition is realized with a special delimiter, this reconfirms us in our view of repetition as happening on a level inbetween a data element and a field, which we might call the level of `occurence'.(8)
In order not to digress too much we decide not to consider data element and field as different things, if we can proof the one to one relation of both. We perform a rewrite on both of them, which is similar to the one we made for `Segment' or `Table'. We'll make this proof when we check the consistency of the database, that we acquired. For now assume, that this proof will succeed.

Figure 2: Model of the HL7 data base before optimization
Figure 2 shows a sort of entity relationship model of the database before we removed multiple occurences. Each relation of the database is graphed as an entity (a name in a box) which has a relation (a line linking it) to an other entity. Note the different notions of `relation', to avoid confusion, we will speak of a `link' if we mean relationships or dependencies between relations. At each contact between a line and a box, there is a number `1' or `n'. This graph can be "read" by following each line with the words: "<number> <name> is linked to <number> <name>" where <number> is the number, which is written at the box of <name>.
Let's have a look if there is more to refine. Were there is a one-to-one link, as between `Table/2' and `Table/3', we can merge the two relations into one, that's what we have already planned to do. However there is more: There is a pair of parallel one-to-many links, one going from `Functional Area' via `Segment/3' and `Field' to `Data Element' and the other going directly from `Functional Area' to `Data Element'. We notice, from the table above, that this parallel link is caused only by the `FunArId' domain. Thus, we can consider removing the domain from the relation at the many-end of the link to remove this indirect redundancy, unless it is not part of a key there, which it isn't. Note that it depends on the one-to-one link, between `Field' and `Data Element' whether we may commit this simplification. If it is a many-to-one link, i.e. if one data element could appear in several fields, we must not do this.
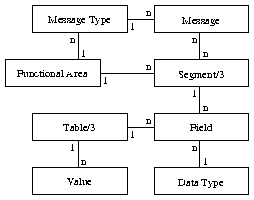
Figure 3: Model of the optimized HL7 data base
Our simplified database looks as sketched in figure 3. The table below will show it in detail: